Regularized Loss Minimization
Chúng ta sẽ hoàn tất những hiểu biết về overfitting và đưa ra một thuật toán supervised learning hiệu quả hơn ERM để chống lại overfitting. Nhưng trước khi đó ta cùng ôn lại những gì đã học ở phần trước bằng một số câu hỏi ngắn như sau:
Q1 : Overfitting là gì?
A1 : Là khi model không có khả năng tổng quát từ những gì đã học được: độ sai sót trên training set nhỏ, trên test set to.
Q2 : Tại sao overfitting lại có hại?
A2 : Vì dữ liệu lúc nào cũng chứa noise. Noise làm cho model tìm được phức tạp quá mức cần thiết.
Q3 : Làm sao để biết được model có bị overfitting hay không?
A3 : Theo dõi learning curve.
Q4 : Làm sao để không bị overfitting?
A4 : Nếu bạn đang nói về chuyện làm sao để $$\mathcal{L}{D{train}}$$ trùng với $$\mathcal{L}{\mathcal{D}}$$ thì câu trả lời là không thể, trừ phi có vô hạn dữ liệu. Đây không phải là một câu hỏi đúng vì overfitting là một khái niệm tương đối, tùy theo "cảm giác" của bạn. "Làm sao để giảm thiểu overfitting?" mới là câu hỏi đúng!_
Nguyên nhân gây ra overfitting
Như chúng ta đã biết, noise không phải là nguyên nhân trực tiếp gây ra overfitting. Vậy những yếu tố nào gây ra overfitting? Overfitting là sản phẩm của sự cộng hưởng giữa các yếu tố sau:
Sử dụng ERM làm objective function. vì objective function và evaluation function có thể rất khác nhau, tối ưu objective function chưa hẳn sẽ tối ưu evaluation function.
Giới hạn về dữ liệu: khi có thêm các cặp observation-label, hiển nhiên ta có thêm thông tin về mối quan hệ giữa chúng. Cụ thể hơn, ta thấy rằng, giả sử dùng cùng một loss function khi train và test, $$\mathcal{L}{D{train}}$$ sẽ hội tụ về $$\mathcal{L}{\mathcal{D}}$$ khi số lượng phần tử của $$D{train}$$ tiến đến vô cùng. Khi hai đại lượng này trùng nhau thì overfitting hoàn toàn biến mất. Vì thế, càng có nhiều dữ liệu huấn luyện thì càng ít bị overfitting.
Model quá "mạnh": một model quá mạnh là khi nó có khả năng mô phỏng rất nhiều mối quan hệ phức tạp giữa observation và label (cũng tức là mô phỏng được rất nhiều dạng hàm số). Ví dụ nếu $$f_w$$ là một đa thức bậc một, nó có thể mô phỏng tất cả các đa thức bậc một (có dạng $$y = f_w(x) = w_1x + w_2$$). Dù có vô số đa thức bậc một, nhưng mà đây được xem như một model "yếu" bởi vì quan hệ tuyến tính được xem như một quan hệ rất đơn giản. Deep neural network được xem là những model mạnh bởi vì chúng mô phỏng được những quan hệ phi tuyến tính. Độ mạnh của model còn phụ thuộc vào cấu trúc và số lượng parameter. Vì bản chất machine learning là ước lượng hàm số, sử dụng một tập model mạnh hơn, thậm chí có khả năng mô phỏng tất cả dạng hàm số tưởng chừng như là một ý hay. Nhưng thực tế đây lại là một ý tưởng này rất tồi. Vì sao?
Vì sao dùng model quá mạnh lại không tốt?
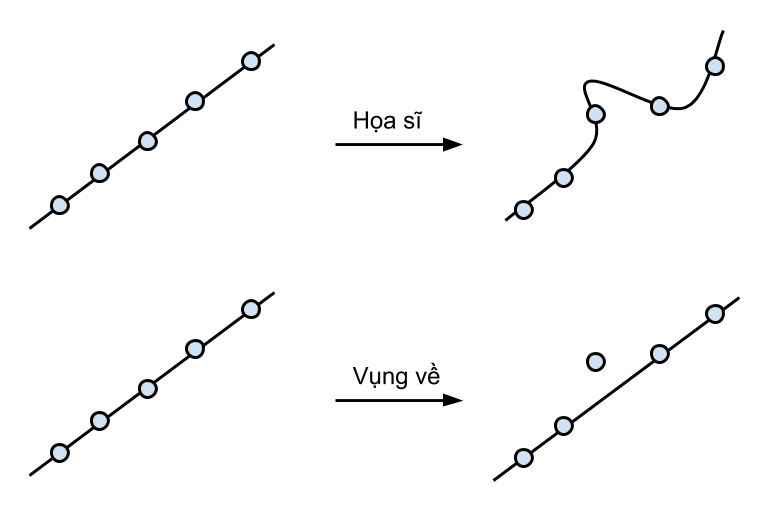
Giả sử có một cuộc thi trong đó ta yêu cầu mỗi thí sinh phải vẽ được một đường đi qua nhiều nhất các điểm cho trước. Thí sinh tham dự có 2 người: một người là họa sĩ, anh ta rất khéo tay và có thể vẽ tất cả các loại đường cong thẳng; người còn lại là một anh chàng vụng về với cây thước kẻ, anh ta chỉ có thể vẽ đường thẳng. Dĩ nhiên là anh họa sĩ sẽ thắng trong trò chơi này.
Nhưng hãy xem xét phản xạ của hai thí sinh trong tình huống sau đây: ta cho đề bài ban đầu là các điểm trên một đường thẳng; sau khi hai người vẽ xong, ta chỉ dịch chuyển một điểm lệch ra khỏi đường thẳng một đoạn nhỏ. Hiển nhiên là ban đầu cả hai người đều vẽ được một đường thẳng đi qua tất cả các điểm. Nhưng sau khi một điểm bị dịch chuyển, anh họa sĩ sẽ vẽ ra một đường hoàn toàn khác với đường thẳng ban đầu để cố đi qua mọi điểm. Ngược lại, anh vụng về thì sẽ vẫn giữ nguyên đáp áp vì đó là đáp án tốt nhất anh có thể vẽ. Điều ta thấy được ở đây đó là anh họa sĩ, vì quá tài hoa, nên anh rất nhạy cảm với những thay đổi nhỏ trong các điểm dữ liệu. Còn anh vụng về, vì năng lực của anh có hạn, nên thường anh sẽ ít bị ảnh hưởng hơn.
Nếu như đây không phải là một cuộc thi vẽ qua nhiều điểm mà là một bài toán machine learning, có lẽ anh họa sĩ đã thua rồi. Bởi vì điểm bị dịch chuyển có thể là do tác động của noise để hòng đánh lừa anh. Anh họa sĩ đại diện cho một tập model cực mạnh, có khả năng mô phỏng mọi hàm số. Một tập model mạnh như vậy rất nhạy cảm với noise và dễ dàng bị overfitting.
Sự kết hợp giữa các yếu tố gây overfitting
Các yếu tố gây ra overfitting phải phối hợp với nhau thì mới đủ điều kiện cho nó xuất hiện. Ta xem xét hai tình huống thường gặp sau:
Có nhiều dữ liệu: ta có thể vô tư dùng ERM, tập model mạnh mà không lo về overfitting. Đây chính là lý do mà thế giới hân hoan khi Big Data xuất hiện.
Làm việc với model yếu: các model thường bị một hội chứng chị em ngược lại với overfitting, gọi là underfitting. Đây là khi model quá đơn giản so với quan hệ cần tìm. Lúc này, dù có tăng thêm dữ liệu cũng không giúp cho model chính xác thêm. Điều cần làm đó là tăng sức mạnh (tăng số lượng tham số hoặc thay đổi dạng) của model.
Mình cũng xin dành ra vài dòng để nói về hiện tượng "cuồng" deep learning và áp dụng deep learning lên mọi bài toán. Các model của deep learning là các neural network cực mạnh nên cần rất nhiều dữ liệu để không bị overfitting. Đó là lý do mà dù các model deep learning này không mới, thậm chí là những model đầu tiên của machine learning, nhưng phải chờ đến kỷ nguyên Big Data hiện tại chúng mới phát huy sức mạnh. Nếu không am hiểu về overfitting và áp dụng deep learning vô tội vạ lên những tập dữ liệu chỉ có vài trăm cặp dữ liệu thì thường đạt đượt kết quả không cao. Khi gặp những điều kiện dữ liệu eo hẹp như vậy, nên bắt đầu từ những model đơn giản như linear model trước. Trong machine learning có một định lý nổi tiếng gọi là "no free lunch" nói rằng không có một model nào tốt nhất cho tất cả các loại dữ liệu. Vì thế, tùy vào bài toán, vào tính chất và số lượng dữ liệu sẵn có, ta mới xác định được model phù hợp.
Regularized loss minimization
Trong bài trước, ta đã biết được một phương pháp để giảm thiểu overfitting, early stopping. Ba yếu tố gây ra overfitting cũng gợi ý cho chúng ta những cách khác để khắc phục vấn đề này. Trong đó, yếu tố thứ hai đưa ra giải pháp đơn giản nhất: tăng kích thước tập huấn luyện. Sau đây, mình sẽ giới thiệu một phương pháp nhằm loại trừ đi yếu tố thứ nhất và thứ ba, được gọi là regularization. Phổ biến nhất, phương pháp này sẽ thêm vào ERM objective function một regularizer nhằm hạn chế sức mạnh của model.
Giả sử rằng đã lỡ tay chọn một model quá mạnh. Thì không cần phải thay đổi dạng model, ta vẫn có thể hạn chế sức mạnh của nó đi bằng cách giới hạn parameter space (không gian của tham số) của model. Xét hai tập model $$A = { fw : w \in X}$$ và $$B = { f{w'} : w' \in Y}$$ chỉ khác nhau về parameter space thôi (ký hiệu $$S = {s : c}$$ đọc là "tập $$S$$ gồm các phần tử $$s$$ sao cho điều kiện $$c$$ thỏa mãn). $$X$$ hoặc $$Y$$ được gọi là không gian tham số của tập model $$A$$ hoặc $$B$$. Trong trường hợp này, nếu $$X \subset Y$$ (X là tập con của Y) thì rõ ràng tập model $$B$$ biểu diễn được mọi hàm số tập model $$A$$ biểu diễn được, tức là $$B$$ mạnh hơn $$A$$.
Nếu parameter $$w$$ là một vector số thực có $$d$$ chiều, tập hợp các giá trị $$w$$ có thể nhận, hay còn gọi là parameter space của $$w$$, là tập tất cả các vector có $$d$$ chiều số thực, ký hiệu là $$\mathbb{R}^d$$. Trong không gian này, mỗi chiều của $$w$$ đều được tự do bay nhảy trong khoảng $$(-\infty,\infty)$$. Muốn thu nhỏ lại không gian này, ta cần một cơ chế để thu hẹp miền giá trị của mỗi chiều.
Để làm được điều đó, ý tưởng ở đây là định nghĩa một đại lượng để khái quát được "độ lớn" của vector $$w$$. Đại lượng này sẽ được dùng làm regularizer, ký hiệu là $$R(w)$$ như ta đã biết, là một hàm số phụ thuộc vào $$w$$. Nó sẽ được gắn thêm vào ERM objective function và được tối thiểu hóa cùng lúc với average loss. Objective function của chúng ta được định nghĩa lại như sau:
$$ \mathcal{L}{D{train}}(fw) = \mathcal{L}{D_{train}}^{ERM} + \lambda R(w)
$$
Tối thiểu hóa objective function này được gọi là quy tắc regularized loss minimization (RLM). Chú ý đối với RLM, không nhất thiết là $$\mathcal{L}{D{train}}^{ERM}$$ phải đạt giá trị tối thiểu để cho objective function trở nên tối thiểu. Nếu một model tối thiểu hóa $$\mathcal{L}{D{train}}^{ERM}$$ nhưng lại làm cho $$R$$ đạt giá trị lớn thì vẫn có cơ hội để chọn một model khác, dù có $$\mathcal{L}{D{train}}^{ERM}$$ lớn hơn nhưng lại cho giá trị của $$R$$ nhỏ hơn nhiều. Nói cách khác, ta có thể lựa chọn được một model đơn giản, dù nó không dự đoán hoàn hảo tập huấn luyện. RLM đang đưa model đi gần đến Occam's razor hết mức có thể, chấp nhận hy sinh độ chính xác trên tập huấn luyện để giảm độ phức tạp của model.
Hằng số $$\lambda$$ trong hàm mục tiêu được gọi là rgularization constant, là một hyperparameter của model. Sự xuất hiện của $$\lambda$$ trong hàm mục tiêu làm cho vai trò của $$\mathcal{L}{D{train}}^{ERM}$$ và $$R$$ trở nên bất đối xứng: nếu ta tăng $$\mathcal{L}{D{train}}^{ERM}$$ lên $$1$$ đơn vị thì hàm mục tiêu tăng lên $$1$$ đơn vị; trong khi đó nếu tăng $$R$$ lên $$1$$ đơn vị thì hàm mục tiêu tăng lên thêm $$\lambda$$ đơn vị. Tức là $$1$$ đơn vị của $$\mathcal{L}{D{train}}^{ERM}$$ có giá trị bằng $$1 / \lambda$$ đơn vị của $$R$$. Thông thường, ta thường đặt $$\lambda$$ rất nhỏ, ví dụ $$\lambda = 10^{-4}$$. Lúc này, $$1$$ đơn vị của $$\mathcal{L}{D{train}}^{ERM}$$ bằng đến $$10^4$$ đơn vị của $$R$$. Điều này thể hiện rằng ta muốn ưu tiên vào tối thiểu hóa $$\mathcal{L}{D{train}}^{ERM}$$ hơn là $$R$$.
Các regularizer thường gặp
$$R(w)$$ thường gặp nhất là norm của vector. Có rất nhiều loại norm, mình sẽ giới thiệu hai loại norm phổ biến nhất.
1-norm (L1-norm): $$ R(w) = ||w||1 = \sum{i = 1}^d |w_i|$$
tức là tổng của trị tuyệt đối của các thành phần. 1-norm đặc biệt ở chỗ là, khi đưa vào hàm mục tiêu, nó sẽ thường cho ra model thưa, tức là model có parameter chứa nhiều chiều bằng 0. Model thưa rất có lợi thế trong tính toán và lưu trữ vì ta chỉ cần làm việc trên các chiều khác 0.
squared 2-norm (L2-norm): $$ R(w) = ||w||2^2 = \sum{i = 1}^d w_i^2$$
cũng còn biết đến với cái tên weight decay, chính là bình phương độ dài của vector $$w$$. Sở dĩ ta phải bình phương là để giúp cho việc tính đạo hàm được dễ hơn khi tối ưu hàm mục tiêu. Lưu ý, đây không thực sự là norm, căn bậc hai của nó mới là norm.